Шта је коефицијент корелације?
Коефицијент корелације користи се да би се утврдило колико је јак однос између две променљиве и његове вредности се могу кретати од -1,0 до 1,0, где -1,0 представља негативну корелацију, а +1,0 представља позитивну везу. Разматра релативна кретања у променљивим и затим дефинише да ли постоји било каква веза између њих.
Формула коефицијента корелације
р = н (Σки) - Σк Σи / √ (н * (Σк 2 - (Σк) 2 )) * (н * (Σи 2 - (Σи) 2 ))
Где
- р = коефицијент корелације
- н = број посматрања
- к = 1. променљива у контексту
- и = друга променљива
Објашњење
Ако постоји било каква корелација или рецимо однос између две променљиве, тада ће назначити да ли се једна од променљивих мења у вредности, онда ће и друга променљива тежити променама вредности, рецимо у одређеној која би могла бити у истој или у супротан смер. Нумерички део једначине спроводи тест и релативну јачину променљивих које се крећу заједно, а називнички део једначине скалира бројилац множењем разлика варијабли са квадратним променљивим.
Примери
Пример # 1
Узмите у обзир следеће две променљиве, к и и, потребне су вам за израчунавање коефицијента корелације.
Испод су дати подаци за прорачун.

Решење:
Користећи горњу једначину, можемо израчунати следеће

Имамо све вредности у горњој табели са н = 4.
Унесите сада вредности за израчунавање коефицијента корелације.

Према томе, прорачун је следећи,

р = (4 * 25,032,24) - (262,55 * 317,31) / √ ((4 * 20,855.74) - (262,55) 2 ) * ((4 * 30,058,55) - (317,31) 2 )
р = 16.820,21 / 16.831,57
Коефицијент ће бити -

Коефицијент = 0,99932640
Пример # 2
Земља Кс је земља са растућом економијом и жели да спроведе независну анализу одлука централне банке које се односе на промене каматних стопа, да ли су оне утицале на инфлацију и да ли централна банка може да их контролише.
Следећи резиме каматне стопе и стопе инфлације која је у просеку владала у земљи тих година дати су у наставку.
Испод су дати подаци за прорачун.

Председник државе вам се обратио да извршите анализу и на следећем састанку одржите презентацију о истој. Користите корелацију и утврдите да ли је централна банка испунила свој циљ или не.
Решење:
Користећи горе разматрану формулу, можемо израчунати коефицијент корелације. Третирање каматне стопе као једне променљиве, рецимо к, и третирање стопе инфлације као друге променљиве као и.

Имамо све вредности у горњој табели са н = 6.
Унесите сада вредности за израчунавање коефицијента корелације.


р = (6 * 170,91) - (46,35 * 22,24) / √ ((6 * 361,19) - (46,35) 2 ) * ((6 * 82,74) - (22,24) 2 )
р = -5,36 / 5,88
Корелација ће бити -

Корелација = -0,92
Анализа: Чини се да је корелација између каматне стопе и стопе инфлације негативна, што се чини као тачан однос. Како каматна стопа расте, инфлација опада, што значи да имају тенденцију да се крећу у супротном смеру једни од других, а из горњег резултата произлази да је централна банка била успешна у спровођењу одлуке која се односи на политику каматних стопа.
Пример # 3
Лабораторија АБЦ спроводи истраживање висине и старости и желела је да зна да ли постоји било каква веза између њих. Окупили су узорак од 1000 људи за сваку од категорија и дошли до просечне висине у тој групи.
Испод су дати подаци за израчунавање коефицијента корелације.

Од вас се тражи да израчунате коефицијент корелације и извучете закључак да ако постоји било какав однос.
Решење:
Третирање старости као једне променљиве, рецимо к, а третирање висине (у цм) као друге променљиве као и.

Имамо све вредности у горњој табели са н = 6.
Унесите сада вредности за израчунавање коефицијента корелације.

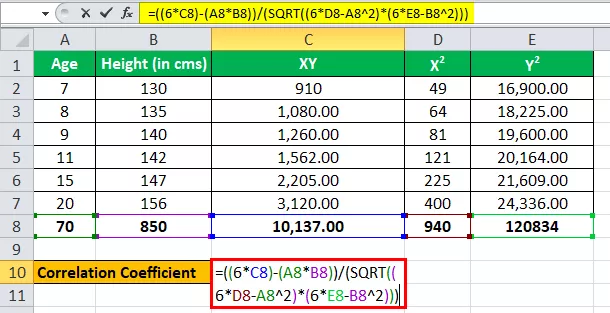
р = (6 * 10,137) - (70 * 850) / √ ((6 * 940 - (70) 2 ) * ((6 * 1,20,834) - (850) 2 )
р = 1.322,00 / 1.361,23
Корелација ће бити -

Корелација = 0,971177099
Релевантност и употреба
У статистикама се користи углавном за анализу снаге односа између променљивих које се разматрају, а даље мери и да ли постоји линеарна веза између датих скупова података и колико би добро могле да буду повезане. Једна од уобичајених мера које се користе у корелацији је Пеарсонов коефицијент корелације.
Ако се променљива промени у вредности и заједно са том променљивом промени у вредности, разумевање те везе је пресудно јер се вредност прве променљиве може користити за предвиђање промене вредности друге променљиве. Корелација у данашње модерно доба има вишеструку употребу, као што се користи у финансијској индустрији, научним истраживањима, а где не. Међутим, важно је знати да корелација има три главне врсте односа. Први је позитиван однос, који наводи ако дође до промене вредности променљиве, тада ће доћи до промене повезане променљиве у истом смеру. Слично томе, ако постоји негативан однос, тада ће се повезана променљива понашати у супротном смеру. Такође, ако не постоји корелација, тада ће р подразумевати нулту вредност.Погледајте слике испод да бисте боље разумели концепт.









